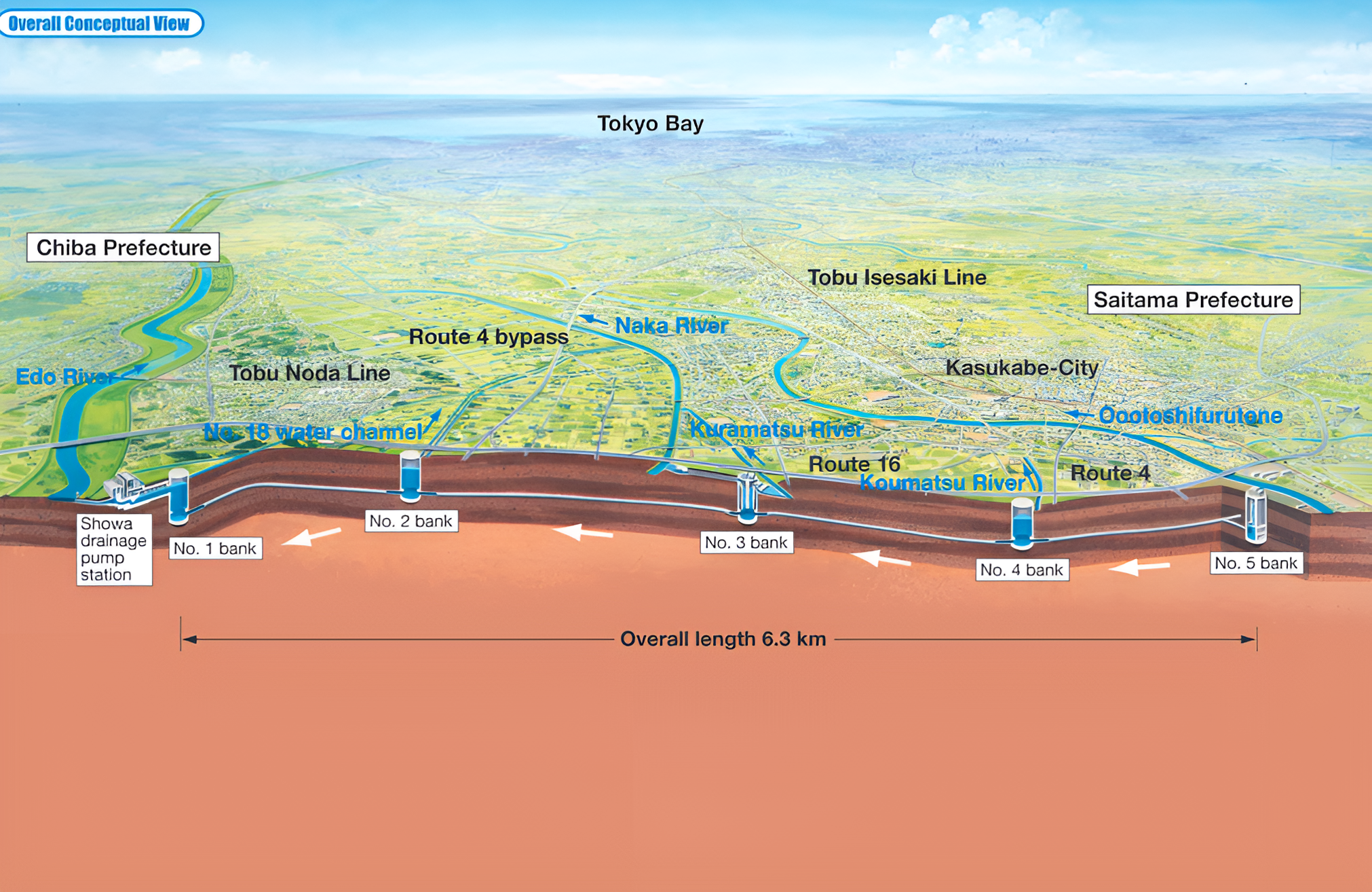
《授时历》是中国古代曾经使用过的一种历法，为元代郭守敬、王恂、许衡等人创制，因古语“敬授人时”而得名。为了编辑历法，郭守敬在当时设立了二十七个测点，最北设在铁勒（今西伯利亚的叶尼塞河流域），最南端设在南海西沙群岛，并派十四个官员到各地观测、记录，费时两年才完成授时历^[1]。从元朝至元十八年（西元1281年）开始实行。明朝所颁行的《大统历》天文数据和推步方法，都依照授时历^[2]，惟《大统历》不计算斗分差（不考虑回归年古长今短），终明之世未改^[3]；可说授时历总共实行了402年。

《授时历》应用弧矢割圆术来处理黄经和赤经、赤纬之间的换算，并用招差术推算太阳、月球和行星的运行度数。《授时历》采用统天历的长度，365.2425日为一年(和地球公转的时间差26秒)，29.530593日为一月，与现在所使用的公历的数值完全相同，但《授时历》比公历早推行301年。推算节气的方法是将一年的¹⁄₂₄作为一气，以没有中气的月份为闰月。它正式废除了古代的上元积年^[4]，而径取至元十八年为为历元，所定的数据全凭实测，打破古代制历的习惯，是中国历法上的大变革之一。

Die Tiermedizin, Tierheilkunde oder Veterinärmedizin (vom französischen Wort vétérinaire), bis ins 20. Jahrhundert auch Tierarznei oder Tierarzneikunde und früher auch Mulomedizin genannt, beschäftigt sich mit den Krankheiten und Verletzungen von Tieren, mit dem Tierschutz und begleitender Forschung, aber auch mit Lebensmitteln tierischer Herkunft und verwandten Themen. Gerade Letzteres ist im Rahmen eines stetig steigenden Verbraucherschutzes von großer Bedeutung, obliegt doch die Kontrolle von Lebensmitteln tierischer Herkunft sowohl in der Erzeugung als auch in der Verarbeitung den Veterinärbehörden.

兽医学（英语：veterinary medicine 或 veterinary science）是一门应用医学诊断与治疗方法来处理动物问题的学门，面对的动物包括宠物、野生动物或家畜与家禽等。兽医学除了研究一般医学问题之外，也关注于动物的行为。受过兽医学训练并以此来诊疗动物的医生称为兽医或兽医师。

兽医学是一门古老的学科。由于一些先进的诊断和治疗技术的出现，兽医学在近年来得到了很大的发展。现在的动物已经可以使用一些先进的方法进行治疗，如注射胰岛素、根管治疗术、髋关节置换术、白内障手术、人工心脏起搏器等牙科或外科的治疗。

Unter Supervisory Control and Data Acquisition (SCADA) versteht man das Überwachen und Steuern technischer Prozesse mittels eines Computer-Systems.

Automationen werden entsprechend dem OSI-Schichtenmodell in mehrere Schichten unterteilt. Dies wird durch die Automatisierungspyramide veranschaulicht.

Dabei ist das Level 1 die prozessnahe Schicht. Der Terminus SCADA bezieht sich gewöhnlich auf zentrale/dezentrale Systeme, die gesamte Installationen überwachen, visualisieren sowie steuern und regeln. Der größte Teil der Regelung wird automatisch durch Fernbedienungsterminals (RTU) oder durch Speicherprogrammierbare Steuerungen (SPS) beziehungsweise Level-1-Automationen durchgeführt.

Die Aufgabe der Level-2-Automation ist es, die Funktion der Level-1-Automation zu optimieren, sowie Stellgrößen und Sollwerte auszugeben. Die Level-3-Automation dient hingegen der Planung, Qualitätssicherung und Dokumentation.

Die Datenerfassung beginnt gewöhnlich mit dem Level 1 und enthält die Koppelung an Messgeräte und Statusinformationen wie Schalterstellungen, die von dem SCADA-System erfasst werden. Die Daten werden dann in einer benutzerfreundlichen Darstellung präsentiert und ermöglichen es, steuernd in den Prozess einzugreifen.

SCADA-Systeme implementieren typischerweise eine verteilte Datenbasis, die Datenpunkte beinhaltet. Ein Datenpunkt enthält einen Ein- oder Ausgangswert, der durch das System überwacht und gesteuert wird. Datenpunkte können physikalisch berechnet werden. Ein physikalischer Datenpunkt stellt einen Eingang oder Ausgang dar, während ein berechneter Punkt durch mathematische Operationen aus dem Zustand des Systems hervorgeht. Normalerweise werden Datenpunkte als eine Kombination von Werten mit Zeitstempel behandelt. Eine Serie von Datenpunkten ermöglicht die historische Auswertung.

Unter Data-Mining [ˈdeɪtə ˈmaɪnɪŋ] (von englisch data mining, aus englisch data ‚Daten‘ und englisch mine ‚graben‘, ‚abbauen‘, ‚fördern‘)^[1] versteht man die systematische Anwendung statistischer Methoden auf große Datenbestände (insbesondere „Big Data“ bzw. Massendaten) mit dem Ziel, neue Querverbindungen und Trends zu erkennen. Solche Datenbestände werden aufgrund ihrer Größe mittels computergestützter Methoden verarbeitet. In der Praxis wurde der Unterbegriff Data-Mining auf den gesamten Prozess der sogenannten „Knowledge Discovery in Databases“ (englisch für Wissensentdeckung in Datenbanken; KDD) übertragen, der auch Schritte wie die Vorverarbeitung und Auswertung beinhaltet, während Data-Mining im engeren Sinne nur den eigentlichen Verarbeitungsschritt des Prozesses bezeichnet.^[2]

Die Bezeichnung Data-Mining (eigentlich etwa „Abbau von Daten“) ist etwas irreführend, denn es geht um die Gewinnung von Wissen aus bereits vorhandenen Daten und nicht um die Generierung von Daten selbst.^[3] Die prägnante Bezeichnung hat sich dennoch durchgesetzt. Die reine Erfassung, Speicherung und Verarbeitung von großen Datenmengen wird gelegentlich ebenfalls mit dem Buzzword Data-Mining bezeichnet. Im wissenschaftlichen Kontext bezeichnet es primär die Extraktion von Wissen, das „gültig (im statistischen Sinne), bisher unbekannt und potentiell nützlich“^[4] ist „zur Bestimmung bestimmter Regelmäßigkeiten, Gesetzmäßigkeiten und verborgener Zusammenhänge“.^[5] Fayyad definiert es als „ein[en] Schritt des KDD-Prozesses, der darin besteht, Datenanalyse- und Entdeckungsalgorithmen anzuwenden, die unter akzeptablen Effizienzbegrenzungen eine spezielle Auflistung von Mustern (oder Modellen) der Daten liefern“.^[2]

Das Schließen von Daten auf (hypothetische) Modelle wird als Statistische Inferenz bezeichnet.

数据挖掘（英语：data mining）是一个跨学科的计算机科学分支^[1][2][3] 。它是用人工智能、机器学习、统计学和数据库的交叉方法在相对较大型的数据集中发现模式的计算过程^[1]。

数据挖掘过程的总体目标是从一个数据集中提取信息，并将其转换成可理解的结构，以进一步使用^[1]。除了原始分析步骤，它还涉及到数据库和数据管理方面、数据预处理、模型与推断方面考量、兴趣度度量、复杂度的考虑，以及发现结构、可视化及在线更新等后处理^[1]。数据挖掘是“数据库知识发现”（Knowledge-Discovery in Databases, KDD）的分析步骤^[4] ，本质上属于机器学习的范畴。

类似词语“资料采矿”、“数据捕鱼”和“数据探测”指用数据挖掘方法来采样（可能）过小以致无法可靠地统计推断出所发现任何模式的有效性的更大总体数据集的部分。不过这些方法可以建立新的假设来检验更大数据总体。

数理经济学（英语：mathematical economics）是运用数学方法来阐述经济学理论和分析经济学问题的学科。从广义上说，数理经济学是运用数学模型来进行经济分析，解释经济学现象的理论。从狭义上来说，是特指法国经济学家瓦尔拉斯（Léon Walras）开创的一般均衡理论体系。通常可分为静态分析与动态分析。

这个理论首先设立“人是理性的”这个假设，然后利用各种数学方法，来模拟各种经济学现象，并进推论出有关问题的解决方案。

Wirtschaftsmathematik ist ein Teilgebiet der Mathematik, das mathematische, insbesondere stochastische Methoden auf wirtschaftliche Fragestellungen anwendet.

In der Mikroökonomie, Makroökonomie und besonders in der Ökonometrie sowie im Operations Research werden mathematische Modelle und Verfahren benutzt, um ökonomische Prozesse zu beschreiben und quantitativ formulierte Probleme zu lösen.

Zum Beispiel werden folgende Aspekte mit Modellen beschrieben:

1. quantitative Untersuchung eines genau definierten ökonomischen Sachverhaltes (Ermittlung einer Konsumfunktion)
2. qualitative Untersuchung eines allgemeinen ökonomischen Prozesses (tendenzieller Verlauf einer Preis-Absatz-Funktion).

Seit 1977 wird Wirtschaftsmathematik von einer Reihe deutscher Universitäten als eigenständiger Studiengang angeboten. Ein Wirtschaftsmathematikstudium ist an Universitäten auch im Studiengang Mathematik mit Nebenfach BWL oder VWL möglich.

Außerdem wird die Lehre der Wirtschaftsmathematik auch in Wirtschaftsschulen (Bayern) in Vorbereitung auf die anderen Wirtschaftsschulfächer, wie beispielsweise BWL, Rechnungswesen etc. angewandt. Als Ausgleich dazu wird das Fach Mathematik in einigen bayerischen Wirtschaftsschulen nur als Wahlfach (in der 9. Jahrgangsstufe 4 Stunden und in der 10. Jahrgangsstufe 3 Stunden a Woche) angeboten.