
漢德百科全書 | 汉德百科全书
 Science and technology
Science and technology


Kriminologie (zusammengesetzt aus lateinisch crimen ‚Verbrechen‘ und -logie von dem griechischen und lateinischen Wort -logia; von altgr. λόγος lógos, ‚Wort‘, auch: ‚Lehre‘,) bedeutet wörtlich übersetzt Lehre vom Verbrechen. Die Kriminologie bedient sich verschiedener Bezugswissenschaften wie Rechtswissenschaften und Psychiatrie, Soziologie und Pädagogik, Psychologie, Ethnologie und Anthropologie, sowie in den letzten Jahrzehnten verstärkt der Wirtschaftswissenschaft, um die Erscheinungsformen der Kriminalität zu beschreiben bzw. zu untersuchen.
In Deutschland ist die universitäre Kriminologie weitgehend den rechtswissenschaftlichen Fakultäten angegliedert. In angloamerikanischen und skandinavischen Ländern sind Kriminologen dagegen überwiegend den sozialwissenschaftlichen Fachbereichen zugeordnet.
Kriminologie ist von der Kriminalistik, der Lehre von den Mitteln und Methoden der Verbrechensbekämpfung, abzugrenzen.
犯罪学(英语:Criminology)是一门社会科学,主题是寻找犯罪行为的现象与规律,寻找犯罪发生的原因,借此寻找方法以减轻犯罪对社会的影响(最后这项于今日已被更精致地分科为刑事政策,而与犯罪学同属刑事学的分支学门)。除了针对犯罪人以外,犯罪学研究也会调查社会与政府对犯罪的认定标准和反应,以及研究如何改善被害人的处境。
在研究方法上,当世的犯罪学特别着重于应用社会学、心理学和经济学的理论及研究方法来观察和了解犯罪现象、成因。此外,随着大脑神经科学和基因的研究兴盛,这两种领域的观点也越来越受犯罪学的欢迎。

Die Funktionalanalysis ist der Zweig der Mathematik, der sich mit der Untersuchung von unendlichdimensionalen topologischen Vektorräumen und Abbildungen auf solchen befasst. Hierbei werden Analysis, Topologie und Algebra verknüpft. Ziel dieser Untersuchungen ist es, abstrakte Aussagen zu finden, die sich auf verschiedenartige konkrete Probleme anwenden lassen. Die Funktionalanalysis ist der geeignete Rahmen zur mathematischen Formulierung der Quantenmechanik[1] und zur Untersuchung partieller Differentialgleichungen.
泛函分析(英语:Functional Analysis)是现代数学分析的一个分支,隶属于分析学,其研究的主要对象是函数构成的函数空间。泛函分析历史根源是由对函数空间的研究和对函数的变换(如傅立叶变换等)的性质的研究。这种观点被证明是对微分方程和积分方程的研究中特别有用。
使用泛函这个词作为表述源自变分法,代表作用于函数的函数,这意味着,一个函数的参数是函数。这个名词首次被雅克·阿达马在1910年使用于这个课题的书中。是泛函分析理论的主要奠基人之一。然而,泛函的一般概念以前曾在1887年是由意大利数学家和物理学家维多·沃尔泰拉(Vito Volterra)介绍。非线性泛函理论是由雅克·阿达马的学生继续研究,特别是莫里斯·弗雷歇(Maurice Fréchet)可和列维(Levy)。
雅克·阿达马还创立线性泛函分析的现代流派,并由弗里杰什·里斯和一批围绕着斯特凡·巴拿赫(Stefan Banach)的波兰数学家群体利沃夫数学学派进一步发展。
 Nobel prize
Nobel prize
 Nobel Peace Prize
Nobel Peace Prize
 Nobel prize
Nobel prize
 Nobel Prize in Chemistry
Nobel Prize in Chemistry
 Nobel prize
Nobel prize
 Nobel Prize in Physiology or Medicine
Nobel Prize in Physiology or Medicine
 Nobel prize
Nobel prize
 University/Institute
University/Institute

 Tennessee-TN
Tennessee-TN

 Universities in the USA
Universities in the USA



Die Kategorientheorie oder die kategorielle Algebra ist ein Zweig der Mathematik, der Anfang der 1940er Jahre zuerst im Rahmen der Topologie entwickelt wurde; Saunders MacLane nennt seine 1945 in Zusammenarbeit mit Samuel Eilenberg entstandene „General Theory of Natural Equivalences“ (in Trans. Amer. Math. Soc. 58, 1945) die erste explizit kategorientheoretische Arbeit. Die Grundbegriffe dieser Theorie sind Kategorie, Funktor und natürliche Transformation. Um den letzteren Begriff zu präzisieren, wurden die ersten beiden ursprünglich eingeführt.
Die Kategorientheorie lässt sich, ähnlich wie die universelle Algebra, als allgemeine Theorie mathematischer Strukturen auffassen (klassische Strukturen sind z. B. Gruppen, Ringe, Moduln und topologische Räume). Dabei werden Eigenschaften mathematischer Strukturen allerdings nicht über Relationen zwischen Elementen der Trägermenge(n) definiert, sondern mittels Morphismen und Funktoren quasi über Vergleiche sowohl innerhalb von als auch zwischen Kategorien.
范畴论(英语:Category theory)是数学的一门学科,是关于数学结构及其关系的一般理论,以抽象的方法处理数学概念,将这些概念形式化成一组组的“对象”及“态射”。数学中许多重要的领域可以形式化为范畴。使用范畴论可以令这些领域中许多难理解、难捉摸的数学结论更容易叙述证明。
一个范畴包含两类数学对象:对象与态射。以集合范畴为例,其对象为集合,态射为集合间的函数。若以第一个态射的目标为源发出第二个态射,这样形成的“复合态射”的性质同复合函数类似(存在结合律与单位态射)。但需注意,范畴的对象不一定要是集合,态射也不一定要是函数;一个数学概念若可以找到一种方法,以符合对象及态射的定义,则可形成一个有效的范畴,且所有在范畴论中导出的结论都可应用在这个数学概念之上。
范畴最简单的例子之一为广群,其态射皆为可逆的。群胚的概念在拓扑学中很重要。范畴现在在大部分的数学分支中都有出现,在理论计算机科学的某些领域中用于对应资料型别,而在数学物理中被用来描述向量空间。
范畴论不只是对研究范畴论的人有意义,对其他数学家而言也有着其他的意思。一个可追溯至1940年代的述语“一般化的抽象废话”,即被用来指范畴论那相对于其他传统的数学分支更高阶的抽象化。

 Education and Research
Education and Research

 Education and Research
Education and Research
 *Important disciplines
*Important disciplines

 Important disciplines
Important disciplines

 Science and technology
Science and technology

Die (medizinische) Radiologie ist das Teilgebiet der Medizin, das sich mit der Anwendung bildgebender Verfahren zu diagnostischen, therapeutischen und wissenschaftlichen Zwecken befasst. Die erste radiologische Abteilung wurde im März 1896 von John MacIntyre, nur Wochen nach der Veröffentlichung von Röntgens Artikel an der Glasgow Royal Infirmary eröffnet.[1]
In den Anfängen der Radiologie wurde ausschließlich das Röntgen mittels Röntgenstrahlen als bildgebendes Verfahren eingesetzt; hiervon leitet sich der Name ab (lateinisch radius ‚Strahl‘). Heute umfasst die Radiologie auch viele weitere bildgebende Verfahren wie die Computertomographie, Sonographie oder Magnetresonanztomographie, unabhängig davon, ob bei diesen Verfahren ionisierende Strahlung zum Einsatz kommt oder nicht.
Zur Diagnostischen Radiologie gehören als Teilgebiete die Neuroradiologie und die Kinderradiologie. Es gibt weitere Schwerpunkte wie die Interventionelle Radiologie. Von Bedeutung für die fachärztliche Tätigkeit des Radiologen sind auch Fragen des Strahlenschutzes und die Auswirkung der Strahlenexposition auf den menschlichen Körper.
Strahlentherapie und Nuklearmedizin sind eng verwandte, aber heute eigenständige Fachgebiete der Medizin, die unter dem Oberbegriff „Strahlenmedizin“ (oder „Strahlenheilkunde“) mit der Radiologie zusammengefasst werden.
Ältere Bezeichnungen für die Radiologie sind Röntgenlehre[2] und Röntgenologie sowie Röntgenkunde; Radiologen wurden auch als Röntgenologen[3] bezeichnet.
影像诊断学(imaging diagnostics[1][2])旧称放射线医学(radiology),是通过特殊手段,展示患者身体内部结构的影像,揭示有无病变及对病变进行定性和/或定量分析,是现代医学极其重要的一个分支,也是现代医学中发展最快,取得成就最多的一部分。
该学科起始于1895年伦琴发现X射线开始,已发展出X线摄影片、利用X光原理再加上电脑运算分析的电脑断层摄影(CT)、利用核磁共振技术的磁共振成像(MRI)、利用超声波原理的超声波造影、借由同位素协助的核子医学造影及正子断层扫描等多种检查工具。此外,各种检查工具针对不同的部位或器官,更发展出许多特别的应用方式,如心导管检查或各器官的血管摄影即是利用在血管内注射显影剂,再用X光原理显像以进行诊断。
影像诊断学除了协助诊断外,亦能协助侵入性诊断甚或是治疗的进行,如超声波造影协助体液抽吸、电脑断层摄影协助脓疡抽吸及肿瘤穿刺生检、以血管摄影协助进行栓塞以止血等。

 Education and Research
Education and Research

 Education and Research
Education and Research
 *Important disciplines
*Important disciplines

 Important disciplines
Important disciplines

 Science and technology
Science and technology
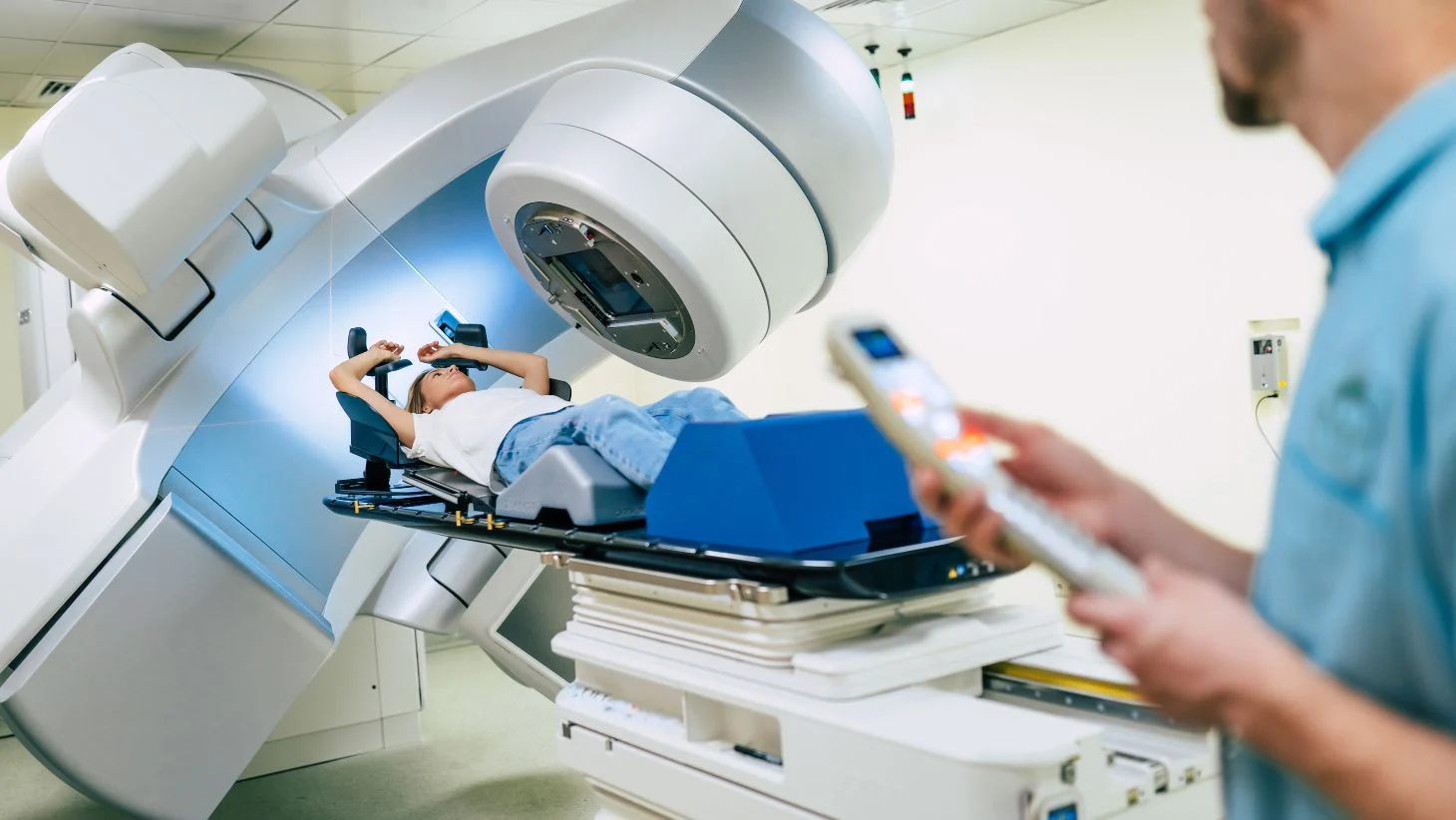
放射肿瘤学,是集合了多学科与高科技技术的一门独立学科,和其他所有学科一样,还在不断发展,不断完善,在今后相当长的时期内仍将为捍卫人类健康继续作出巨大贡献。放射治疗(英语:radiation therapy,radiotherapy)简称放疗,是一种治疗癌症的方式,原理为使用由直线加速器或放射性核种制造的高能电离辐射来控制或破坏恶性细胞。放射治疗可以治愈一些仅在特定身体部分内存在的癌症,也可以用作辅助治疗,在手术切除原发恶性肿瘤后防止肿瘤复发(例如治疗早期阶段的乳腺癌)。放射治疗与化疗之间可以协同使用,易感癌症的化疗之前、期间和之后都可能使用放射治疗。肿瘤学中与放射治疗有关的亚专业被称为放射肿瘤学。从事这一子专业的医生被称作放射肿瘤学家。
Strahlentherapie (auch Radiotherapie) oder Strahlenbehandlung ist die medizinische Anwendung von ionisierender Strahlung auf den Menschen und auf Tiere, um Krankheiten zu heilen oder deren Fortschreiten zu verzögern. Die Strahlung kann aus Geräten oder aus radioaktiven Präparaten stammen. Fachgebiete für diese spezielle Anwendung von Strahlung heißen Strahlenheilkunde und Radioonkologie.
Als Strahlen werden vorwiegend Gammastrahlung, Röntgenstrahlung und Elektronenstrahlung verwendet. In den letzten Jahren wurden auch Anlagen zur Behandlung mit Neutronen, Protonen und schweren Ionen (häufig Kohlenstoff-Ionen) errichtet. Nicht ionisierende Strahlen wie zum Beispiel Mikrowellen- und Wärmestrahlen, Licht- und UV-Therapie sowie die Behandlung mit Ultraschallwellen werden der Strahlentherapie nicht zugeordnet.
Strahlentherapie umfasst die Behandlung von gut- und bösartigen Erkrankungen. Sie wird von Fachärzten für Radiologie oder für Strahlentherapie unter Mitwirkung von medizinisch-technischen Radiologieassistenten und spezialisierten Medizinphysikern ausgeübt. Ihre Tätigkeit unterliegt der länderspezifischen Gesetzgebung im Strahlenschutz und den nachgeordneten Verordnungen (vgl. Strahlenschutzverordnung) und Normen. Der eigentlichen Therapie geht ein komplexer Planungsprozess – die Bestrahlungsplanung – voraus. Umfangreiche organisatorische und technische Qualitätssicherungsmaßnahmen sorgen dafür, dass Bestrahlungsfehler weitgehend ausgeschlossen werden können.
Nach den in Deutschland gültigen Weiterbildungsordnungen umfasst das Gebiet Strahlentherapie auch die medikamentösen und physikalischen Verfahren zur Radiosensibilisierung und Verstärkung der Strahlenwirkung am Tumor (Radioimmuntherapie und Radiochemotherapie), unter Berücksichtigung von Schutzmaßnahmen der gesunden Gewebe.


 Australia
Australia
 Belgium
Belgium
 Brazil
Brazil
 Germany
Germany
 Finland
Finland
 France
France
 Iran
Iran
 Israel
Israel
 Italy
Italy
 Japan
Japan
 Canada
Canada
 New Zealand
New Zealand
 Norwegen
Norwegen
 Austria
Austria
 Russia
Russia
 Sweden
Sweden
 United States
United States
 United Kingdom
United Kingdom
 Vietnam
Vietnam

 Science and technology
Science and technology

Die Fields-Medaille, offizieller Name International Medal for Outstanding Discoveries in Mathematics (deutsch: „Internationale Medaille für herausragende Entdeckungen in der Mathematik“), ist eine der höchsten Auszeichnungen, die ein Mathematiker erhalten kann. Sie ist benannt nach ihrem Stifter, dem kanadischen Mathematiker John Charles Fields (1864–1932), und wurde das erste Mal 1936 vergeben. Seit 1950 wird sie alle vier Jahre von der Internationalen Mathematischen Union (IMU) anlässlich des Internationalen Mathematikerkongresses (ICM) an zwei bis vier Mathematiker verliehen, die jünger als 40 Jahre sind und sich in besonderer Weise auf dem Gebiet der mathematischen Forschung hervorgetan haben (so formell definiert seit 1966). Mit der Verleihung ist ein Preisgeld von 15.000 kanadischen Dollar verbunden. Beim ICM werden gleichzeitig drei weitere Preise verliehen: der Carl-Friedrich-Gauß-Preis für Beiträge zur angewandten Mathematik, die IMU-Abakus-Medaille für Beiträge zur theoretischen Informatik und die Chern-Medaille für herausragendes Lebenswerk auf höchstem Niveau.
菲尔兹奖(英语:Fields Medal),正式名称为国际杰出数学发现奖(英语:International Medals for Outstanding Discoveries in Mathematics),是一个在国际数学联盟的国际数学家大会上颁发的奖项。每四年评选2-4名有卓越贡献且年龄不超过40岁的数学家。得奖者须在该年元旦前未满四十岁。
奖项以加拿大数学家约翰·查尔斯·菲尔兹的名字命名。菲尔兹筹备设立该奖,并在遗嘱中捐出47,000元给奖项基金。
菲尔兹奖被认为是年轻数学家的最高荣誉,和阿贝尔奖均被称为数学界的诺贝尔奖。奖金有15,000加拿大元,约合13,767美元。而阿贝尔奖的奖金有600万瑞典克朗,约合100万美元,更接近诺贝尔奖。

菲利波·布鲁内莱斯基(意大利语:Filippo Brunelleschi,“Brunelleschi”又译布鲁内列斯基、伯鲁乃列斯基,1377年—1446年4月15日),意大利文艺复兴早期颇负盛名的建筑师与工程师,他的主要建筑作品都位于意大利佛罗伦萨。根据他的熟人兼传记作者安东尼奥·马内蒂的说法:布鲁内莱斯基“得以享有埋葬在圣母百花大教堂的殊荣,在世时已经雕好一个大理石胸像,以这样一个辉煌的墓志铭作为永恒的纪念。”
Filippo Brunelleschi (* 1377 in Florenz; † 15. April 1446 ebenda) war ein in Florenz aktiver Bildhauer, Architekt und Ingenieur des 15. Jahrhunderts. Zu seinen Werken als Baumeister gehören das Findelkinderhaus (Ospedale degli Innocenti), die Alte Sakristei von San Lorenzo und die Kuppel der Kathedrale von Florenz (Santa Maria del Fiore). Gemeinsam mit Lorenzo Ghiberti nahm er 1401 am Wettbewerb für das Bronzeportal des Florentiner Baptisteriums teil, in dem er jedoch unterlag.
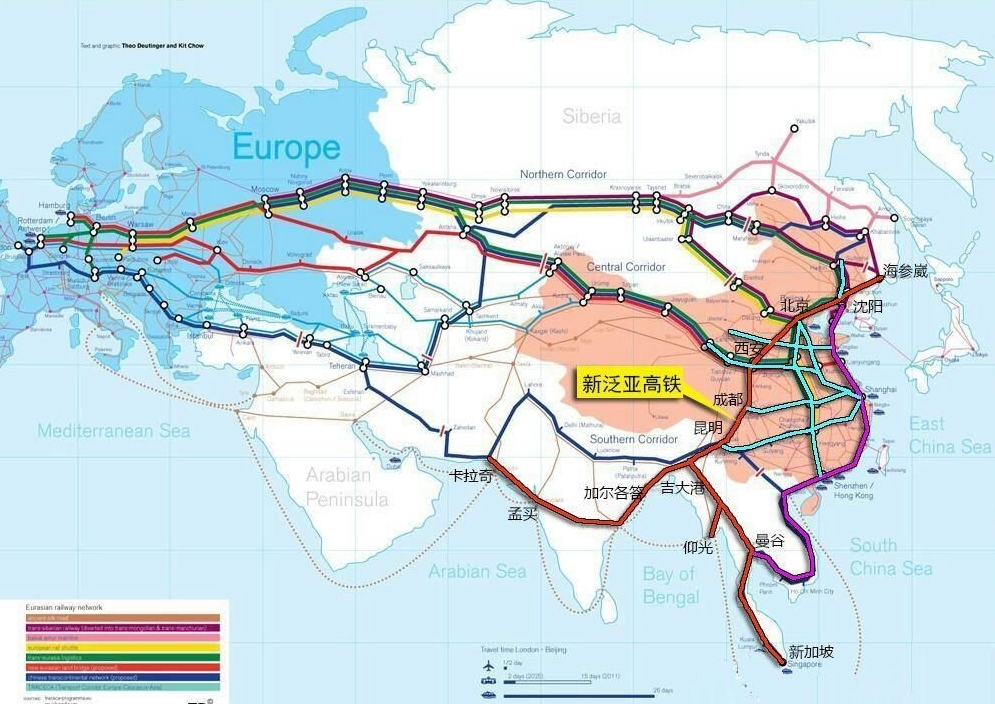
 Transport and traffic
Transport and traffic
 Geography
Geography
 Vacation and Travel
Vacation and Travel


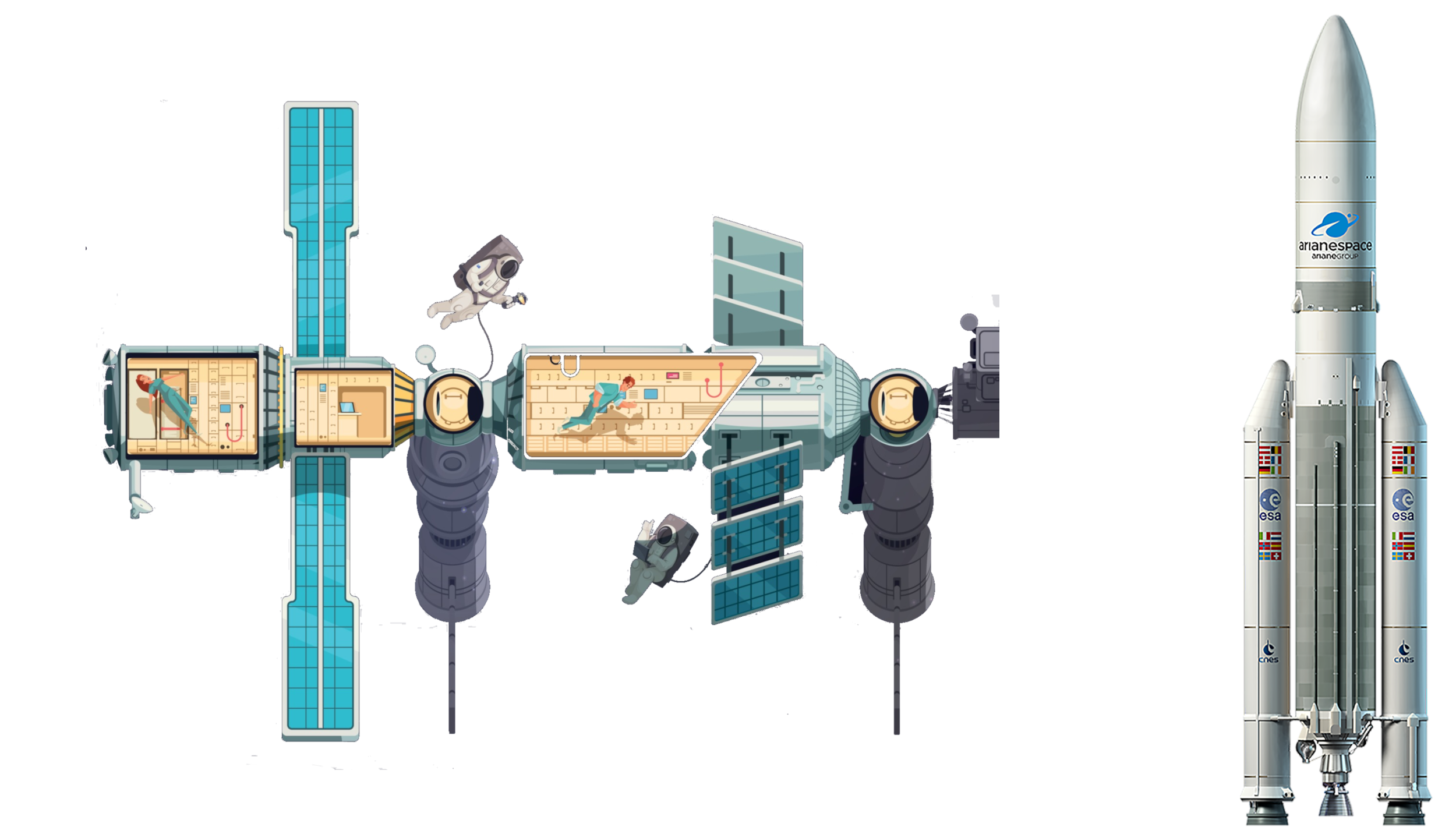 Aerospace
Aerospace
 Astronomy
Astronomy
 California-CA
California-CA
 Medical, Pharmaceutical, Rehabilitation
Medical, Pharmaceutical, Rehabilitation


 Automobile
Automobile
 History
History
 Companies
Companies
 IT-Times
IT-Times
 Life and Style
Life and Style