My channels - Wissenschaftler in der Aufklärung

Sir Isaac Newton [ˌaɪzək ˈnjuːtən] (* 25. Dezember 1642jul. / 4. Januar 1643greg. in Woolsthorpe-by-Colsterworth in Lincolnshire; † 20. März 1726jul. / 31. März 1727greg. in Kensington)[1] war ein englischer Physiker, Astronom und Mathematiker an der Universität Cambridge und Leiter der Royal Mint. Wie erst später öffentlich bekannt wurde, beschäftigte er sich ebenfalls mit theologischen, historischen und alchemistischen Untersuchungen.
Isaac Newton ist der Verfasser der Philosophiae Naturalis Principia Mathematica, in denen er mit seinem Gravitationsgesetz die universelle Gravitation beschrieb und die Bewegungsgesetze formulierte, womit er den Grundstein für die klassische Mechanik legte. Fast gleichzeitig mit Gottfried Wilhelm Leibniz entwickelte Newton die Infinitesimalrechnung. Er verallgemeinerte das binomische Theorem mittels unendlicher Reihen auf beliebige reelle Exponenten. Bekannt ist er auch für seine Leistungen auf dem Gebiet der Optik: die von ihm verfochtene Teilchentheorie des Lichtes und die Erklärung des Lichtspektrums.
Aufgrund seiner Leistungen, vor allem auf den Gebieten der Physik und Mathematik (siehe Geschichte der Physik, Geschichte der Mathematik), gilt Sir Isaac Newton als einer der bedeutendsten Wissenschaftler aller Zeiten. Die Principia Mathematica werden als eines der wichtigsten wissenschaftlichen Werke eingestuft.
Eine Sammlung von Schriften, im Bestand der National Library of Israel, zu theologischen und alchemistischen Themen wurde 2015 von der UNESCO zum Weltdokumentenerbe erklärt.

Gottfried Wilhelm Leibniz (* 21. Junijul. / 1. Juli 1646greg. in Leipzig, Kurfürstentum Sachsen; † 14. November 1716 in Hannover, Kurfürstentum Braunschweig-Lüneburg) war ein deutscher Philosoph, Mathematiker, Jurist, Historiker und politischer Berater der frühen Aufklärung. Er gilt als der universale Geist seiner Zeit und war einer der bedeutendsten Philosophen des ausgehenden 17. und beginnenden 18. Jahrhunderts sowie einer der wichtigsten Vordenker der Aufklärung. Im 18. Jahrhundert wird er vielfach als „Gottfried Wilhelm Freiherr von Leibniz“ bezeichnet; jedoch fehlt bislang eine Beurkundung über eine Nobilitierung.
In frühen Schriften anderer Autoren wurde sein Nachname – analog zu demjenigen seines Vaters, Friedrich Leibnütz, und dessen väterlichen Vorfahren – auch „Leibnütz“, teils auch „Leibnitz“ (franz. Godefroi Guillaume Leibnitz) geschrieben.[1] Sein Name wurde auch in verschiedenen Versionen latinisiert, z. B. als Godefridus Guilelmus Leibnitius. Ab 1671 wählte er die Schreibweise „Leibniz“ für seinen Familiennamen.
geboren: 25. Januar 1736 in Turin
gestorben: 10. April 1813 in Paris
Senator von Frankreich
1801 Auswärtiges Mitglied der Göttinger Akademie der Wissenschaften;
1808 Auswärtiges Mitglied der Bayerischen Akademie der Wissenschaften
Lagrange besuchte das Turiner Kolleg, wo er mit siebzehn das erste mathematische Interesse zeigte, nachdem er zufällig auf eine Veröffentlichung Edmund Halleys stieß. In der Schule interessierte sich Lagrange schließlich mehr für Mathematik, speziell die Geometrie. Er brachte sich innerhalb eines Jahres das gesamte Wissen eines vollständig ausgebildeten Mathematikers seiner Zeit bei.
Mit 19 Jahren erhielt er einen Lehrstuhl für Mathematik an der Königlichen Artillerieschule in Turin. Hier veröffentlichte er seine ersten wissenschaftlichen Arbeiten über Differentialgleichungen und Variationsrechnung.
Dem Ruf Friedrichs II. von Preußen folgend ging Lagrange 1766 als Nachfolger von Leonhard Euler als Direktor an die Königlich-Preußische Akademie der Wissenschaften nach Berlin.
Ab 1795 lehrte er für kurze Zeit an der École Normale Supérieure und trat in das neu gegründete Institut de France ein. Ab 1797 lehrte er an der École polytechnique.
Lagrange begründete die analytische Mechanik (Lagrange-Formalismus mit der Lagrange-Funktion), die er 1788 in seinem berühmten Lehrbuch Mécanique analytique darstellte. Weitere Arbeitsgebiete waren das Dreikörperproblem der Himmelsmechanik (Lagrange-Punkte), die Variationsrechnung und die Theorie der komplexen Funktionen. Er leistete Beiträge zur Gruppentheorie (bevor diese als eigener Forschungszweig existierte) und zur Theorie der quadratischen Formen in der Zahlentheorie. In der Analysis ist die lagrangesche Darstellung des Restgliedes der Taylor-Formel und in der Theorie der Differentialgleichungen die Lagrange-Multiplikatorenregel bekannt.
Lagrange ist im Panthéon aufgebahrt. Er ist namentlich auf dem Eiffelturm verewigt.

Geboren am 15. April 1707 in Basel als Sohn eines Pfarrers, studierte Leonhard Euler an der Universität Basel zunächst Philosophie und Theologie, bevor er sich dem Studium der Mathematik bei Johann Bernoulli zuwandte. Nachdem der Versuch in Basel eine Professur zu erhalten gescheitert war, folgte er 1727 einem Ruf an die zwei Jahre zuvor eröffnete St. Petersburger Akademie der Wissenschaften. Zunächst wirkte er hier als Adjunkt, ab 1730 als Professor für Physik und nach der Rückkehr Daniel Bernoullis nach Basel im Jahre 1733 als Professor für Mathematik.
Arbeit an der Preussischen Akademie der Wissenschaft
In den politischen Wirren von 1741 nahm Euler ein Angebot von Friederichs II. von Preussen an und übersiedelte nach Berlin, wo er einen wesentlichen Anteil am Aufbau der Preussischen Akademie der Wissenschaften leistete. Hier bekleidete Euler das Amt des Direktors der Mathematischen Klasse, pflegte aber weiterhin enge Kontakte mit St. Petersburg. Unzufrieden mit seiner Behandlung durch Friedrich II., nahm Euler 1766 den erneuten Ruf an die St. Petersburger Akademie, der im Namen der Zarin Katharina II. erfolgt war, an. Trotz einer schweren Augenkrankheit, die zu einer vollständigen Erblindung führte, blieb er bis zu seinem Tod am 18. September 1783 überaus produktiv und übte einen massgeblichen Einfluss auf die Tätigkeit der Akademie aus.
Dokument

Exlibrisstempel «R. Wolf» aus: Leonhard Euler: Vollständige Anleitung zur Algebra. St. Petersburg: bei der Kaiserlichen Akademie der Wissenschaften, 1771, Titelseite. ETH-Bibliothek, Alte und Seltene Drucke, Rar 4961.
Werke
Leonhard Euler gilt als einer der bedeutendsten Mathematiker überhaupt. Er verfasste über 900 Arbeiten, davon rund 40 Monografien. Die Bandbreite seiner wissenschaftlichen Tätigkeit ist heute unvorstellbar. Euler lieferte massgebliche Beiträge zur Algebra (Zahlentheorie, Analysis), Mechanik und Physik, Geometrie und Trigonometrie, Astronomie, Schiffbau, Artillerie und Architektur sowie Philosophie, Musiktheorie und Theologie. Euler gilt als Begründer der Analysis. In seinem Grundlagenwerk Introductio in analysin infinitorum wurde zum ersten Mal der Begriff der «Funktion» verwendet. Entsprechend geht ein grosser Teil der modernen mathematischen Symbolik auf Euler zurück. Zudem wurden nach Euler zahlreiche mathematische Phänomenecall_made benannt.

J. Ackeret: Untersuchung einer nach den Euler’schen Vorschlägen (1754) gebauten Wasserturbine, in: Schweizerischen Bauzeitung, Band 123 (1944), Nr.1, S. 3.
Die Euler-Turbine
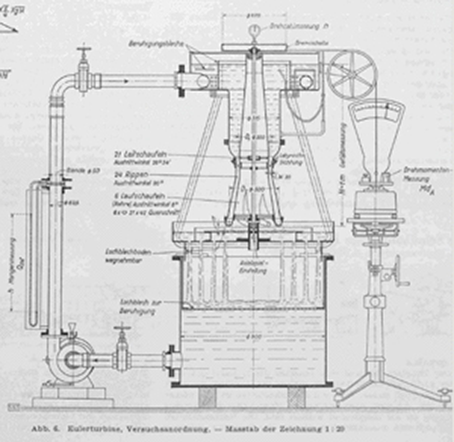
Dabei war er seiner Zeit weit voraus, wie das Beispiel der Euler-Turbine zeigt. Die rein theoretischen Berechnungen Eulers aus dem 18. Jahrhundert versuchte der bekannte Aerodynamiker Jakob Ackeret 1944 an der ETH Zürich in die Praxis umzusetzen. Die bei der Firma Escher-Wyss nachgebaute Turbine wies einen respektablen Wirkungsgrad auf, wie der Artikel von Ackeret in der Schweizerischen Bauzeitungcall_made zeigt.
Die unglaubliche Produktivität Eulers beschäftigt die Mathematiker noch heute. Bei der Gesamtausgabe handelt es sich um ein Jahrhundertwerk der Schweizerischen Akademie der Wissenschaftencall_made, das noch immer nicht abgeschlossen ist.
Bestand
Die ETH-Bibliothek besitzt zahlreiche zeitgenössische und moderne Ausgaben von Eulers Werken. Über das Suchportal der ETH-Bibliothek sind Monografien such- und bestellbar. Die unselbständigen Abhandlungen sind in den Opera Omnia zu finden. 12 Monographien sind auch als E-Texte elektronisch verfügbar.
